composed of resistors and capacitors driven by a voltage or current source. A first order RC circuit is composed of one resistor and one capacitor and is the simplest type of RC circuit.
RC circuits can be used to filter a signal by blocking certain frequencies and passing others. The two most common RC filters are the high-pass filters and low-pass filters; band-pass filters and band-stop filters usually require RLC filters, though crude ones can be made with RC filters.
The simplest RC circuit is a capacitor and a resistor in series. When a circuit consists of only a charged capacitor and a resistor, the capacitor will discharge its stored energy through the resistor. The voltage across the capacitor, which is time dependent, can be found by using Kirchhoff's current law, where the current charging the capacitor must equal the current through the resistor. This results in the linear differential equation
 .
.
The time required for the voltage to fall to
 is called the RC time constant and is given by
is called the RC time constant and is given byComplex impedance
The complex impedance, ZC (in ohms) of a capacitor with capacitance C (in farads) is represents the imaginary unit:
represents the imaginary unit:
 is the exponential decay constant (in radians per second), and
is the exponential decay constant (in radians per second), and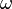 is the sinusoidal angular frequency (also in radians per second).
is the sinusoidal angular frequency (also in radians per second).
Sinusoidal steady state
Sinusoidal steady state is a special case in which the input voltage consists of a pure sinusoid (with no exponential decay). As a result,Series circuit

Series RC circuit
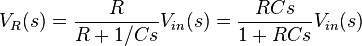 .
.
Transfer functions
The transfer function from the input voltage to the voltage across the capacitor is .
.
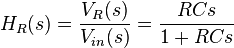 .
.
Poles and zeros
Both transfer functions have a single pole located at .
.
Gain and phase
The magnitude of the gains across the two components are: ,
,
 .
.

 .
.
Current
The current in the circuit is the same everywhere since the circuit is in series:Impulse response
The impulse response for each voltage is the inverse Laplace transform of the corresponding transfer function. It represents the response of the circuit to an input voltage consisting of an impulse or Dirac delta function.The impulse response for the capacitor voltage is
Similarly, the impulse response for the resistor voltage is
Frequency-domain considerations
These are frequency domain expressions. Analysis of them will show which frequencies the circuits (or filters) pass and reject. This analysis rests on a consideration of what happens to these gains as the frequency becomes very large and very small.As
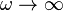 :
:
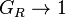 .
.
 :
:
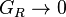 .
.
The range of frequencies that the filter passes is called its bandwidth. The point at which the filter attenuates the signal to half its unfiltered power is termed its cutoff frequency. This requires that the gain of the circuit be reduced to
 .
.
Clearly, the phases also depend on frequency, although this effect is less interesting generally than the gain variations.
As
 :
:
 .
.
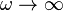 :
:Time-domain considerations
- This section relies on knowledge of e, the natural logarithmic constant.
 and
and 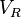 given above. This effectively transforms
given above. This effectively transforms  . Assuming a step input (i.e.
. Assuming a step input (i.e.  before
before  and then
and then  afterwards):
afterwards): .
.
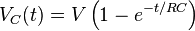
 .
.
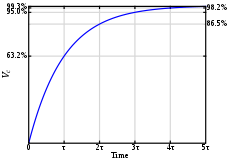
Thus, the voltage across the capacitor tends towards V as time passes, while the voltage across the resistor tends towards 0, as shown in the figures. This is in keeping with the intuitive point that the capacitor will be charging from the supply voltage as time passes, and will eventually be fully charged.
These equations show that a series RC circuit has a time constant, usually denoted
 being the time it takes the voltage across the component to either rise (across C) or fall (across R) to within
being the time it takes the voltage across the component to either rise (across C) or fall (across R) to within  of its final value. That is,
of its final value. That is,  is the time it takes
is the time it takes  to reach
to reach  and
and 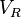 to reach
to reach  .
.The rate of change is a fractional
 per
per  . Thus, in going from
. Thus, in going from  to
to  , the voltage will have moved about 63.2% of the way from its level at
, the voltage will have moved about 63.2% of the way from its level at  toward its final value. So C will be charged to about 63.2% after
toward its final value. So C will be charged to about 63.2% after  , and essentially fully charged (99.3%) after about
, and essentially fully charged (99.3%) after about  . When the voltage source is replaced with a short-circuit, with C fully charged, the voltage across C drops exponentially with t from
. When the voltage source is replaced with a short-circuit, with C fully charged, the voltage across C drops exponentially with t from 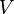 towards 0. C will be discharged to about 36.8% after
towards 0. C will be discharged to about 36.8% after  , and essentially fully discharged (0.7%) after about
, and essentially fully discharged (0.7%) after about  . Note that the current,
. Note that the current,  , in the circuit behaves as the voltage across R does, via Ohm's Law.
, in the circuit behaves as the voltage across R does, via Ohm's Law.These results may also be derived by solving the differential equations describing the circuit:
 .
.
Integrator
Consider the output across the capacitor at high frequency i.e. .
.
 given above:
given above: which is just Ohm's Law.
which is just Ohm's Law.
 ,
,
Differentiator
Consider the output across the resistor at low frequency i.e.,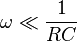 .
.
 again, when
again, when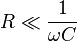 ,
,
More accurate integration and differentiation can be achieved by placing resistors and capacitors as appropriate on the input and feedback loop of operational amplifiers (see operational amplifier integrator and operational amplifier differentiator).
Parallel circuit

Parallel RC circuit
 is equal to the input voltage
is equal to the input voltage  — as a result, this circuit does not act as a filter on the input signal unless fed by a current source.
— as a result, this circuit does not act as a filter on the input signal unless fed by a current source.With complex impedances:
 .
.
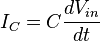 .
.
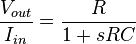 .
.

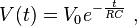

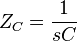



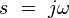






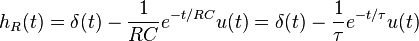












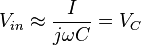

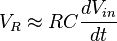


No comments:
Post a Comment