- Sometimes we are not sure in electric circuits that the resistors are neither in parallel nor in series. See the circuit below here the relation between R1 resistor and R6resistor is series or parallel we are not sure.

- In that case we can simplify this circuit using three terminal equivalent networks. Three terminal networks are used in three phase connection, matching networks and electrical filters.


These networks are the equivalent of large network. I will discuss here how to transform wye to delta and delta to wye.
- Delta to wye conversion
-It is easy to work with wye network. If we get delta network, we convert
it to wye to work easily. To obtain the equivalent resistance in the
wye network from delta network we compare the two networks and we
confirm that they are same. Now we will convert figure 3 (a) delta
network to figure 2 (a) wye network.
From figure 3 (a) for terminals 1 and 2 we get,
-R12 (∆) = Rb || (Ra + Rb)
From figure 2 (a) for terminals 1 and 2 we get,
-R12(Y) = R1 + R3
Setting wye and delta equal,
-R12(Y) = R12 (∆) we get,
-R12 (∆) = Rb || (Ra + Rb)
From figure 2 (a) for terminals 1 and 2 we get,
-R12(Y) = R1 + R3
Setting wye and delta equal,
-R12(Y) = R12 (∆) we get,
Equations (v), (vi) and (vii) are the equivalent resistances for
transforming delta to wye conversion. We do not need to memorize these
equations. Now we create an extra node shown in figure 4 and follow the
conversion rule,
Each
resistor in the Y network is the product of the resistors in the two
adjacent Del branches, divided by the sum of the three Del resistors.

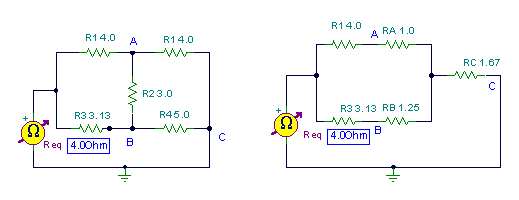
Now we will solve a problem how to convert delta to wye network. It will give clear concept.
Problem: convert the delta network to wye network.

From equation (v), (vi) and (vii) we can find the equivalent resistance of wye network,
The equivalent Y network configuration is shown in figure 6.

Wye to delta conversion
For conversion to wye network to delta network adding equations (v), (vi) and (vii) we get,
R1R2 + R2R3 + R3R1 = RaRbRc(Ra +Rb + Rc)/(Ra + Rb + Rc)2
= RaRbRc/(Ra + Rb + Rc) —————— (ix)
Dividing equation (ix) by each of the equations (v), (vi) and (vii) we get,
Ra = R1R2 + R2R3 + R3R1/ R1
Rb = R1R2 + R2R3 + R3R1/ R2
Rc = R1R2 + R2R3 + R3R1/ R3
For Y to delta conversion the rule is followed below,
Each
resistor in the delta network is the sum of all possible products of Y
resistors taken two at a time, divided by the opposite Y resistor.
Delta and Y are said to be equal or balanced when
R1 = R2 = R3 = RY, Ra = Rb = Rc = R∆
For these condition conversion formulas become,
RY = R∆/3
Or R∆ = 3RY
Here Y connection is like series connection. And Del is like parallel connection.
Wye(Y) & Delta(Δ)
- This article is about the mathematical technique. For the device which transforms three-phase electric power without a neutral wire into three-phase power with a neutral wire, see delta-wye transformer. For the application in statistical mechanics see, see Yang–Baxter equation. For the regional airline brand name for Delta Air Lines, see Delta Connection.
The Y-Δ transform can be considered a special case of the star-mesh transform for three resistors.
Y-Δ transform
The Y-Δ transform is known by a variety of other names, mostly based upon the two shapes involved, listed in either order. The Y, spelled out as wye, can also be called T or star; the Δ, spelled out as delta, can also be called triangle, Π (spelled out as pi), or mesh. Thus, common names for the transformation include wye-delta or delta-wye, star-delta, star-mesh, or T-Π.
Basic Y-Δ transformation
Equations for the transformation from Δ-load to Y-load 3-phase circuit
The general idea is to compute the impedance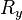 at a terminal node of the Y circuit with impedances
at a terminal node of the Y circuit with impedances 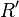 ,
,  to adjacent node in the Δ circuit by
to adjacent node in the Δ circuit by are all impedances in the Δ circuit. This yields the specific formulae
are all impedances in the Δ circuit. This yields the specific formulaeEquations for the transformation from Y-load to Δ-load 3-phase circuit
The general idea is to compute an impedance in the Δ circuit by
in the Δ circuit bywhere
is the sum of the products of all pairs of impedances in the Y circuit and
 is the impedance of the node in the Y circuit which is opposite the edge with
is the impedance of the node in the Y circuit which is opposite the edge with  . The formula for the individual edges are thus
. The formula for the individual edges are thusCircuit Analysis: Techniques for Solving Δ-load to Y-load in 3 phase circuits
A given three phase circuit that has a combination of Δ-loads and Y-loads should be converted to the Y configuration. By converting from Δ to Y, each circuit element/phase can be analyzed separately. Converting from Δ to Y is an technique aimed to simplify circuit analysis. (Note: harmonic behavior from the original circuit remained unchanged). The conversion from the Δ notation to Y notation is as follows.Wye-Delta Conversion
In many circuits, resistors are neither in series nor in parallel, so the rules for series or parallel circuits described in previous chapters cannot be applied. For these circuits, it may be necessary to convert from one circuit form to another to simplify the solution. Two typical circuit configurations that often have these difficulties are the wye (Y) and delta (D) circuits.Wye to Delta
For a circuit like this (Y):
We can convert it to (D):
To obtain the value for Ra, Rb and Rc:
Ra= (R1)(R2)+(R1)(R3)+(R2)(R3)
R1
Rb= (R1)(R2)+(R1)(R3)+(R2)(R3)
R2
Rc= (R1)(R2)+(R1)(R3)+(R2)(R3)
R3
R1= (Rb)(Rc)
Ra+Rb+Rc
R2= (Ra)(Rc)
Ra+Rb+Rc
R3= (Ra)(Rb)
Ra+Rb+Rc
Take a look at the following example:
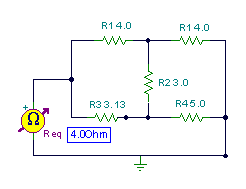
Find the equivalent resistance of the circuit:
Notice that the resistors are connected neither in series nor in parallel, so we can't use the rules for series or parallel connected resistors
Let's choose the delta of R1,R2 and R4:and convert it to a star circuit of RA, RB, RC.
Using Wye to Delta, we would get:
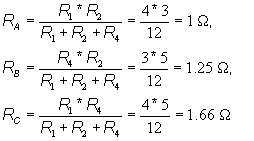












No comments:
Post a Comment